The
data of Gause on interaction of two species of yeast:
Lotka-Volterra’s
interspecific competition or product inhibition?
Hadi Farazdaghi
89 Willcocks St., Toronto, ON. M5S 1C9 Canada
email hadi@farazdaghi.com
Note: The Site is shared with readers like you. Please feel free to leave your Comments.
Please click on
for PDF version.
Abstract:
An examination is made of the growth and interaction of two alcohol producing species of yeast, Schizosaccharomyces "Kephir” and Saccharomyces cerevisiae in both monoculture and mixture as reported by Gause (1934. The struggle for existence. Williams and Wilkins, Baltimore, M.D.) and modeled by de Wit and Goudriaan (1978. Simulation of ecological processes. A Halsted Press Book. John Wiley & Sons, New York, Toronto.), on the basis of Lotka-Volterra competition model.
The logistic equation of growth has been integrated to represent the inhibition of growth of each species by alcohol in pure culture. This model is expanded for mixed culture, based on the relative inhibition of each species by the other. The proposed model for pure anaerobic culture produces results identical to Lotka-Volterra model for both organisms. For mixed culture, the model shows that both species reach the potential levels expected by the model. However, the relative growth rates of the two organisms are affected differently, one, (Kephir), behaves exactly according to the model, and the other, (S.cerevisiae), exhibits considerable reduction in relative growth rate. This interaction also confirms the general conclusion of de Wit & Goudriaan that in addition to alcohol, some other factor must be involved in mixed culture of the two species. .
Last revision July 9, 2004
Copyright ã Hadi Farazdaghi (2004)
Introduction.
The logistic equation represents a relationship for the growth of living organisms with time. In this relationship, the initial growth increases as a power or exponential function of time, in which the growth gradually slows down and approaches a constant maximum level determined by the genetic and environmental potentials. This equation can be written as:
P = Pm /(1+k.e -R.t ) 1
or, in derivative form as:
dP/dt = R.P.(1- P/Pm) 2
Equation 2 has also been written in the following form:
dP/dt = A.p – B.P2 3
where P is the amount of growth and pm its maximum value; R is the relative growth rate of the organism, t is time and d denotes derivative. The values of k, A, and B are constant parameters, and e is the base for natural logarithm. The logistic equation of growth is valid when the external factors remain constant.
Gause (1934) performed a number of experiments, growing two species of yeast, Schizosaccharomyces "Kephir” and Saccharomyces cerevisiae, in pure and mixed cultures. Under aerobic conditions both species consume sugar and as long as the conditions are maintained the reproductive growth continues. When the conditions become anaerobic, even with ample supply of sugar and essential elements, alcohol is produced which reduces reproduction. The reproduction ultimately stops when the alcohol concentration reaches a critical level. However, the concentrations of alcohol up to the critical level are not detrimental to the existence of the yeasts. Gause found that both the “growth rate” (dP/dt), and the “potential growth” (Pm), of the two species in terms of bud formation are influenced and limited by the amount of alcohol in the medium in both pure and mixed cultures. Gause proposed that the reduction in growth of both populations was affected by the amount of alcohol that was produced.
The data of Gause have been studied by de Wit and Goudriaan (1978) who, decided to “analyse whether this explanation is acceptable by constructing a model that simulates the growth of two species independently and in mixture, under the assumption that the production of the same harmful product is the only cause of interaction.” (de Wit & Goudriaan 1978, page 22). In order to simulate the growth of these two species, they used a set of two differential equations known as Lotka-Volterra logistic equations, as follows:
dP1/dt = R1.P1.(1-A1.P1 – B1.P2) 4
dP2/dt = R2.P2.(1-A2.P1 – B2.P2) 5
where subscripts 1 & 2 denote organism 1 and 2 respectively. Equations 4 and 5 have been proposed by Lotka (1925) and Volterra (1931), to describe the growth and survival of two species living in the same environment, and interacting as predator and prey. Because of this type of interaction, the equations are given in differential forms and cannot be integrated for simulation of their interaction. De Wit & Goudriaan (1978), assumed that the conditions of Lotka-Volterra apply to those of the yeasts of Gause experiments, and consider that “… this set of differential equations cannot be integrated into analytical expressions” for P1 and P2 as functions of time. Therefore, they used differential equations 4 and 5 directly in a CSMP program to simulate the growth of the organisms in pure and mixed cultures (see Appendix 1). Jeffers (1978) also followed the same steps, using a BASIC computer language program, which yielded similar results.

The simulations of de Wit & Goudriaan (1978) for anaerobic pure and mixed
cultures are given in Fig 1a and Fig.1b respectively.
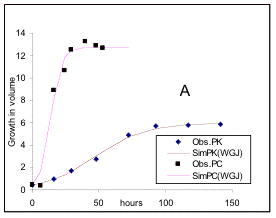
Fig 1. Experimental data of Gause (1934) for the growth of (symbols) Kephir (K) and S.cerevisae(C), in both pure (P), and mixed (M) cultures with respect to time (hours), and simulation (sim) results (lines), for each culture by de Wit & Goudriaan (1978). Simulation results of Jeffers (1978) are also the same (WGJ).
From comparing the simulation results with the experimental data of Gause, The above authors noted that while the simulation results for pure culture of either species of fungi closely resemble the experimental data, the results for mixed cultures are markedly different. In fact the maximum growth obtained from the simulation models for Kephir in mixed culture is almost one half of that of observed values, while the maximum growth of S.cerevisae is considerably larger than the simulated values (see Fig. 1a and b).
de Wit & Goudriaan (1978) concluded their studies by suggesting that, this discrepancy has been the result of an interaction between the two species. In their view, one of the species should have suppressed the growth of the other one by production of some harmful compound in addition to alcohol.
Although the conclusions reached by the authors seem reasonable, we would like to re-examine the problem by viewing it from other angles and explore if we can further clarify the nature of the interaction.
Analysis:
a) Interaspecific Competition in
Pure Culture:
1- The first question is the validity of the similarity of the coexistence and interaction of these two organisms with those of predator and prey of Lotka-Volterra. To the extent that we know, these two organisms neither compete for food, nor their physical existence is threatened by alcohol. It is the accumulation of alcohol, as a waste product, that reduces the growth rates of each species and finally stops their growth. This may be in considerable variance with the interaction of predator and prey, which directly influences the number of prey, and through that, their future growth rate and interaction with predator. Therefore, the equations of Lotka-Volterra can be integrated for this particular case, if we can find a satisfactory model for their inter-relationship. However, this variation alone cannot make any considerable change in the results, and logically we should reach the same conclusion whether we use the differential or integrated forms of the equations.
2, In equations of Lotka-Volterra (eqns 4 & 5) A1, A2, B1, and B2 are considered as constant growth reduction factors. We further explore the relationship between these constants, to see whether they are independent constants or complex parameters. First, we write the differential form of the logistic equation, for mono-culture of the two species, in the following forms:
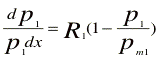 6
6
and
 7
7
where, Pm1 and Pm2 are the maximum growth, or the potential that can be achieved by species 1 and 2 under the given environmental conditions of mono-culture. This is based on the assumption that the rate of alcohol production, which inhibits the reproductive growth of each species in monoculture, is proportional to the growth of that species. This assumption has also been used by de Wit & Goudriaan. Furthermore, the growth stops under a given concentration of alcohol, which suggests that, under anaerobic conditions, the growth potential is controlled and limited by alcohol concentration. This conclusion permits the use of logistic equation. However, logistic equation has two independent constant parameters, i.e. pm and R as shown in equations 6 or 7. Therefore, it would be of interest to see how these two parameters are influenced in mixed culture for each one of the species. As the rates of alcohol production by the two species are proportional to their growth, therefore, it does not make any difference if we consider either the growth or the alcohol production of each species in an inhibition or competition model.
Equation 6 or 7 can be written in the following forms:
 8
8
and then integrated with initial conditions assuming that at ti =0, p = pi, we get:

1/P = 1/Pm + ( 1/Pi – 1/Pm)e –Rt
9
Equation 9 can be used for the growth of organisms in pure culture with respect to time.
A test of equation 9 for the growth of each species in pure culture is given in Fig 2.
Fig 2. The squares and diamonds represent observed data for pure anaerobic cultures of Kephir and S.cerevisiae respectively. The initial amounts for both species is 0.45; RK = 0.054, and RC = 0.23; Pmc=12.8 and Pmk= 6. Simulation lines, which are almost identical, are from de Wit & Goudriaan (1978), Fig 1a, and the analytical model (equation 9), presented in the text.
The close proximity of the simulated graph from equation 9 (SimPCF and SimPKF), with both the experimental data of Gause and the simulation lines of de Wit & Goudriaan for both species, demonstrate the validity of the model for interaspecific competition in pure cultures.
b) Interspecific Competition in
Mixed Culture:
Considering that growth rates of single organisms in relation to substrates, and their inhibition is largely similar to those of enzymes, by using this analogy, it would be useful to explore if it is possible to develop a model for the growth of the two species in a mixed culture.
It is known that, in pure culture, both species come to equilibrium with a specific concentration of alcohol (1.5%), at which their reproduction is ceased. This level sets a maximum potential for the growth of each of the two organisms. This potential limit was used, together with the relative growth rate, to describe the growth of each species in pure culture, from a given initial conditions (equation 9). If we use the analogy of enzyme kinetics, from equation 6 or 7, the inhibition constant of alcohol can be defined, using:
Ki = Pm/R 10
Therefore, we define a relative inhibition factor for the two species of yeast as follows:
a=Kik/Kic 11
and
b=Kic/Kik 12
in which “a” can relate the inhibition constant of Kephir relative to that of cerevisiae, and “b” is the inverse of a. Therefore, assuming that the amount of alcohol is negligible for both species at the initial conditions, from equation 9, we write:
1/Pc = 1/(Pmc-a.Pc) + ( 1/Pi – 1/(Pmc –a.Pc)e –Rct 13
in which a.Pc is equivalent to the inhibitory effect of Kephir on potential production of cerevisiae. After simplifications we get:
a.Pc2 – Pc[(a+1)Pi.eRct + Pmc-Pi] + Pmc.Pi. eRct = 0 14
A similar equation can also be written for Kephir.
b.Pk2 – Pk [(b+1)Pi.eRkt
+ Pmk-Pi] + Pmk.Pi. eRkt
= 0
15
This formulation is based on the assumption that there are no other interacting
factors except the alcohol. The
constant parameters considered for the two species in mixed
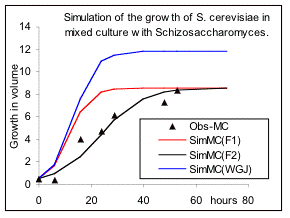
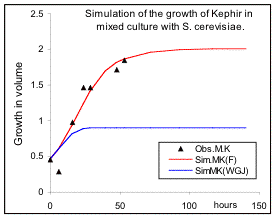
Fig 3. The influence of mixed culture on the rates of reproduction of Kephir (Schizosaccharomysis) and S. cerevisiae. See text for details.
culture are the same as before, but the response equations have changed to equations 14 and 15 for S.cerevisiae and Kephir respectively, and thus the parameter “a” and its inverse “b” are calculated on the basis of the parameters in pure culture. The simulation results are presented in Fig 3a and Fig.3b for the two species (red lines). The results suggest that the effects of mutual inhibition is applicable to Kephir, but for S.cerevisiae, (left figure), it can only describe the inhibition of the maximum growth, and the rate of growth for achieving the maximum is different. This confirms the views of de Wit & Goudriaan that the growth of two species should be influenced by an additional interacting factor. Further test suggests that the relative growth rate of S.cerevisiae has been reduced by a factor equivalent to the inhibition constant for this organism (black line). Whether this has been through an initial shock at the beginning of the treatment or a secretion of poisonous compounds by Kephir, we don’t know. Note that Lotka-Volterra model provides under-estimation in one case and over- estimation in another one. It is clear that equations 9, 14 and 15, that were derived on the basis of the strength of the relative inhibition of the two species, provide very reasonable results for both pure and mixed cultures.
Acknowledgement: The author wishes to thank Dr. J. Goudriaan for his kind permission to use information from de Wit & Goudriaan (1978).
Appendix:
Information used in the CSMP program of de Wit & Goudriaan (1978).
Initial conditions ( organism volume = 0.45)
Maximum alcohol production = MALC= 1.5
Growth Rate = GR = Relative Growth Rate (R)*P1(1-RED), with R1=0.21, and R2=0.06.
Where RED is the reduction factor due to alcohol;
RED1 = AFGEN (RED1T, ALC/MALC)
Where AFGEN is an arbitrary function generator, for a given time T, and alcohol level (ALC), relative to the maximum alcohol production (MALC), and used a linear function:
FUNCTION RED1T = (0,0), (1.,1.)
With ALC = INTRL (IALC, ALCP1)
The initial conditions for alcohol is IALC = 0, and alcohol production rate, (ALCP), is proportional to the growth rate.
ALCP1 = ALCPF1.GR1 and ALC = INTGRL (IALC, ALCP1 + ALCP2)
ALCPF1=0.12, and ALCPF2=0.26;
References:
Gause, G.F., 1934. The struggle for existence. Williams and Wilkins, Baltimore, M.D.
Jeffers, J.N.R. 1978. An introduction to systems analysis with ecological applications. Pp 198, University Park Press, MD21202
Lotka, A.J., 1925. Elements of physical ecology. Williams and Wilkins, Baltimore, M.D.
Volterra, V. 1926. Variazioni e fluttuazioni del numero d'individui in specie animali conviventi. Mem. R. Accad. Naz. dei Lincei. Ser. VI, vol. 2.
Volterra,V. 1931. Variations and fluctuations of the number of individuals in animal species living together. In R.N. Chapman, ‘Animal ecology’, McGraw-Hill, New York.
Wit, C.T. de, and Goudriaan, J.(1978). Simulation of ecological processes. A Halsted Press Book. John Wiley & Sons, New York, Toronto.